Contributions
With the
availability of wireless networks and inexpensive mobile devices, continuously
monitoring of spatial queries over moving data objects has become a
necessity to many recent location-based applications. Consequently, a number
of techniques [SR01,TP02,TPS02,ZZP$^+$03,ISS03,XMA$^+$04,YPK05,HXL05,MHP05]
have been developed to efficiently process continuous 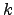 nearest neighbor (
nearest neighbor (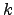 NN)queries
and its variants. Below we summarize the contributions of this thesis to the continuous
monitoring of spatial queries3.
NN)queries
and its variants. Below we summarize the contributions of this thesis to the continuous
monitoring of spatial queries3.
- For continuous monitoring of spatial queries, the interest of database community
has been shifted towards using grid based index because R-tree
cannot handle object updates very efficiently. We design CircularTrip and ArcTrip, two novel
grid access methods that traverse grid cells according to their proximity to the query point.
- We propose CircularTrip-based algorithm [CYL07] to continuously monitor
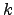 NN queries
and our extensive experiments demonstrate that our approach is
NN queries
and our extensive experiments demonstrate that our approach is  to
to  times
faster than CPM [MHP05] which is currently the best known algorithm for continuous
times
faster than CPM [MHP05] which is currently the best known algorithm for continuous 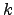 NN
queries. Moreover, we prove that our CircularTrip based algorithm accesses the minimum
number of cells during the continuous monitoring of
NN
queries. Moreover, we prove that our CircularTrip based algorithm accesses the minimum
number of cells during the continuous monitoring of 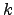 NN queries.
NN queries.
- Our CircularTrip based algorithm is not only time efficient but it is also
space efficient. Its space usage is
 to
to  of CPM's space requirements.
of CPM's space requirements.
- We present the techniques based on CircularTrip and ArcTrip to continuously
monitor other variants of
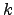 NN queries like constrained nearest neighbor queries,
farthest neighbor queries and (
NN queries like constrained nearest neighbor queries,
farthest neighbor queries and (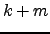 ) nearest neighbor queries.
Our proposed techniques can easily be extended
to answer any complex query that is hybrid of above mentioned queries. For example, our algorithms can
be used to continuously monitor (
) nearest neighbor queries.
Our proposed techniques can easily be extended
to answer any complex query that is hybrid of above mentioned queries. For example, our algorithms can
be used to continuously monitor (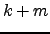 ) farthest neighbors in a constrained region where the spatial
conditions that constrain the region can be changed by the user at any time.
Moreover, our proposed algorithms preserve the
properties that all the algorithms have low memory requirements and the number of cells
accessed for each type of query is minimum.
) farthest neighbors in a constrained region where the spatial
conditions that constrain the region can be changed by the user at any time.
Moreover, our proposed algorithms preserve the
properties that all the algorithms have low memory requirements and the number of cells
accessed for each type of query is minimum.
- We give a detailed survey of previous work on spatial
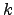 nearest neighbor queries and
its popular variants.
nearest neighbor queries and
its popular variants.
Muhammad Aamir Cheema
2007-10-11
![]() nearest neighbor (
nearest neighbor (![]() NN)queries
and its variants. Below we summarize the contributions of this thesis to the continuous
monitoring of spatial queries3.
NN)queries
and its variants. Below we summarize the contributions of this thesis to the continuous
monitoring of spatial queries3.