Motivation
A grid based index evenly partitions the
space into cells. The extent of each cell  on each dimension is
on each dimension is  .
.
![$ c[i, j]$](img254.png) indicates the cell at column
indicates the cell at column  and row
and row  and the lower-left
corner cell of the grid is
and the lower-left
corner cell of the grid is ![$ c[0, 0]$](img257.png) . Clearly, point
. Clearly, point  with location coordinates
(
with location coordinates
( ) falls into the cell
) falls into the cell
![$ c[\lfloor p.x / \delta \rfloor, \lfloor p.y / \delta \rfloor]$](img259.png) . An example of
grid based index is shown in Figure
. An example of
grid based index is shown in Figure ![[*]](./icons/crossref.png) . Compared with other
complicated spatial indexes (e.g.,
. Compared with other
complicated spatial indexes (e.g.,  -tree)
grid based index is simple and can be maintained efficiently in the dynamic
environment.
The order in which cells of grid are accessed is important for efficient
monitoring of the NN queries hence a need is to develop an access method which minimizes
the number of cells accessed. The minimum number of cells that are needed to be accessed
to answer any
-tree)
grid based index is simple and can be maintained efficiently in the dynamic
environment.
The order in which cells of grid are accessed is important for efficient
monitoring of the NN queries hence a need is to develop an access method which minimizes
the number of cells accessed. The minimum number of cells that are needed to be accessed
to answer any 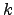 NN query q are only the cells that lie or intersect the circle with center
NN query q are only the cells that lie or intersect the circle with center 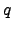 and radius
and radius  (the shaded cells in Fig.
(the shaded cells in Fig. ![[*]](./icons/crossref.png) ),
where
),
where  is the distance of
is the distance of  NN from
NN from 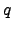 .
Any algorithm that visits a cell that lies outside the circle, visits
a cell which cannot have any result object. In contrast, any algorithm that does not access any
cell that lies or intersects the circle may potentially miss a valid result object. To the best
of our knowledge, CPM [MHP05] provides the only method that tries to minimize the number of
cells accessed. CPM minimizes the number of cells accessed in initial computation of any
.
Any algorithm that visits a cell that lies outside the circle, visits
a cell which cannot have any result object. In contrast, any algorithm that does not access any
cell that lies or intersects the circle may potentially miss a valid result object. To the best
of our knowledge, CPM [MHP05] provides the only method that tries to minimize the number of
cells accessed. CPM minimizes the number of cells accessed in initial computation of any 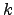 NN
query by employing a conceptual partitioning of grid into rectangles and using a heap as discussed
in details in Section
NN
query by employing a conceptual partitioning of grid into rectangles and using a heap as discussed
in details in Section ![[*]](./icons/crossref.png) . However,
CPM accesses unnecessary cells during handling of the updates. Moreover, it also needs to
store some data structure for each registered query
. However,
CPM accesses unnecessary cells during handling of the updates. Moreover, it also needs to
store some data structure for each registered query 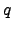 .
.
Figure:
Grid Index
|
![\includegraphics[bb=215 341 379 505]{kNN/fig/grid_example.eps}](img260.png)
|
Figure:
Minimal Set of Cells
|
![\includegraphics[bb=215 341 379 505]{kNN/fig/minCells.eps}](img261.png)
|
CPM partitions the space into conceptual rectangles and the rectangles do not
reflect spatial proximity to any point. We note that circle centered at query point represents the better proximity
and we use this intuition to develop our grid access methods.
We design CircularTrip and ArcTrip that access the cells according to
their proximity to 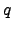 and minimize the number of cells accessed not only in initial computation
of results but also during the updates handling of nearest neighbor queries.
and minimize the number of cells accessed not only in initial computation
of results but also during the updates handling of nearest neighbor queries.
CircularTrip: Given a radius  , CircularTrip returns all the cells that intersect the circle
of radius
, CircularTrip returns all the cells that intersect the circle
of radius  with center at
with center at 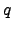 .
.
ArcTrip: Given a radius  and an angle range
and an angle range
 , ArcTrip returns all the cells that intersect the circle of radius
, ArcTrip returns all the cells that intersect the circle of radius  with center at
with center at 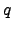 and lie between angle range
and lie between angle range
 .
.
In next chapters, we will show how these
access methods can be used to continuously monitor 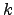 NN queries and its variants (i.e., constrained NN queries).
We show that by using our access method, these queries can be answered while maintaining the following properties
NN queries and its variants (i.e., constrained NN queries).
We show that by using our access method, these queries can be answered while maintaining the following properties
- The number of cells accessed to continuously monitor
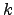 NN query and its variants is minimum. i.e;
it does not visit any unnecessary cell even during the handling of updates.
NN query and its variants is minimum. i.e;
it does not visit any unnecessary cell even during the handling of updates.
- As opposed to CPM, there is no need to store any additional data structure for each query.
We also prove that our proposed access methods computes the
 exactly the same number of
times as the number of cells it returns. Below in Table
exactly the same number of
times as the number of cells it returns. Below in Table ![[*]](./icons/crossref.png) we summarize the math notations used
throughout this thesis.
we summarize the math notations used
throughout this thesis.
Muhammad Aamir Cheema
2007-10-11
![]() and minimize the number of cells accessed not only in initial computation
of results but also during the updates handling of nearest neighbor queries.
and minimize the number of cells accessed not only in initial computation
of results but also during the updates handling of nearest neighbor queries.
![]() , CircularTrip returns all the cells that intersect the circle
of radius
, CircularTrip returns all the cells that intersect the circle
of radius ![]() with center at
with center at ![]() .
.
![]() and an angle range
and an angle range
![]() , ArcTrip returns all the cells that intersect the circle of radius
, ArcTrip returns all the cells that intersect the circle of radius ![]() with center at
with center at ![]() and lie between angle range
and lie between angle range
![]() .
.
![]() NN queries and its variants (i.e., constrained NN queries).
We show that by using our access method, these queries can be answered while maintaining the following properties
NN queries and its variants (i.e., constrained NN queries).
We show that by using our access method, these queries can be answered while maintaining the following properties
![]() exactly the same number of
times as the number of cells it returns. Below in Table
exactly the same number of
times as the number of cells it returns. Below in Table ![]() we summarize the math notations used
throughout this thesis.
we summarize the math notations used
throughout this thesis.