thesis

$\begin{approval} \vspace*{5mm} \begin{center} \par This thesis entitled \par \vs... ... Date ................................... \par \end{approval}$

$\begin{copyright} \par I hereby grant the University of New South Wales or its a... ... Date ................................... \par \end{copyright}$

$\begin{originality} \par I hereby declare that this submission is my own work an... ... Date ................................... \par \end{originality}$

$\begin{dedication} \par I dedicate this thesis to my parents who have always bee... ...ways surrounds me and never lets any sadness enter inside. \par \end{dedication}$ ¹ ²

$\begin{acknowledgements} \par I am very thankful to my parents for their love, s... ... reverse nearest neighbors over the time period $T$. \par \end{acknowledgements}$

Abstract:

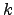
nearest neighbor query

retrieves

objects that lie closest to the query point

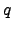
among a given set of objects

. With the availability of inexpensive location aware mobile devices, the continuous monitoring of such queries has gained lot of attention and many methods have been proposed for continuously monitoring the

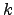
NNs in highly dynamic environment. Multiple continuous queries require real-time results and both the objects and queries issue frequent location updates. Most popular spatial index, R-tree, is not suitable for continuous monitoring of these queries due to its inefficiency in handling frequent updates. Recently, the interest of database community has been shifting towards using grid-based index for continuous queries due to its simplicity and efficient update handling. For

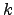
NN queries, the order in which cells of the grid are accessed is very important. In this research, we present two efficient and effective grid access methods, CircularTrip and ArcTrip, that ensure that the number of cells visited for any continuous

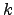
NN query is minimum. Our extensive experimental study demonstrates that CircularTrip-based continuous

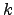
NN algorithm outperforms existing approaches in terms of both efficiency and space requirement. Moreover, we show that CircularTrip and ArcTrip can be used for many other variants of nearest neighbor queries like constrained nearest neighbor queries, farthest neighbor queries and (

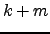
)-NN queries. All the algorithms presented for these queries preserve the properties that they visit minimum number of cells for each query and the space requirement is low. Our proposed techniques are flexible and efficient and can be used to answer any query that is hybrid of above mentioned queries. For example, our algorithms can easily be used to efficiently monitor a (

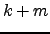
) farthest neighbor query in a constrained region with the flexibility that the spatial conditions that constrain the region can be changed by the user at any time.